Time Value of Money

The time value of money takes account of changes to the financial value of money over time. In order to understand this concept it may help to first consider the analogy of the more commonly known phenomenon of inflation. When the rate of inflation is high money loses real purchasing power quickly. Similarly, the higher the interest rates in financial markets, the less valuable is future money in terms of money of today.

Inflation is a change in the ratio of the amount of money chasing goods and services. Where money growth exceeds the one of productivity, the real value of money drops. In contrast, time value of money is exclusively concerned with the reproduction of money through interest within the financial system.

Figure 1 shows an example bank account earning 4% of interest. While its nominal value keeps growing along the green line, its present value shown in black is flat-lining. This is because the conversion of future or past money balances to present time value reverts the effects of compound interest.

Present and Future Value

Reverting compound interest effects by discounting back to present value is the essence of the concept of time value of money. Present and future values of current account balances follow from compound interest calculation. Assuming constant interest rates with discrete compounding, the relevant formulas are:

\begin{gather*}
FV(t)=PV \cdot (1+\frac{1}{m}\cdot r_i)^{t \cdot m}\\
\\
PV=FV(t) \cdot (1+\frac{1}{m}\cdot r_d)^{-t \cdot m}\\
\end{gather*}

\begin{alignat*}{2}
FV(t):~&& &\mathrm{future ~ value}\\
&& &\mathrm{at ~ time} \space t\\
PV:~&& &\mathrm{present ~ value}\\
&& &(\mathrm{at ~ time} \space 0)\\
m: ~&& & \mathrm{compounding}\\
 && & \mathrm{frequency}\\
r_i: ~&& & \mathrm{interest \space rate}\\
r_d: ~&& & \mathrm{discount \space rate}\\
\end{alignat*}

While the future value FV is an exponential growth, the present value PV is the inverse, an exponential decline^[1]. Therefore, when the interest rate r_i is same as the discount rate r_d, then the present value of an interest earning balance remains constant through time.

Time value of money is the basis for the pricing of a multitude of consumer credit, retirement savings and retail banking services. For instance, the pricing of annuities is an application of discounting to present value. Though most textbook examples assume the equality of investment interest r_i and discount interest r_d, they almost always differ in retail banking. Just compare offers on high interest savings accounts and mortgages to see this.

Time Value versus Real Value

Since time value of money is a matter of interest rates within the financial system, its relation to the real economy is often neglected. However, it’s real purchasing power that should matter most to retail banking clients.

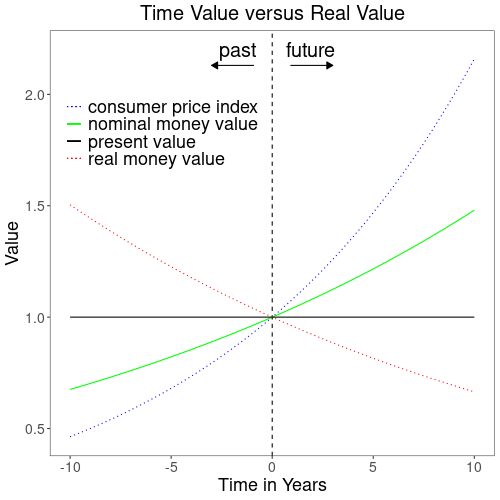
As of writing this article in November 2022, the US and the EU are experiencing a period of financial repression^[2]. During normal economic times the real interest rate, which is defined as the difference between nominal interest and inflation, is positive. Without real interest, incentives for lending and saving are lacking. Therefore, financial markets should naturally adjust interest rates to top inflation. And politics are financially repressive if they don’t allow this to happen.

Figure 2 illustrates the situation that citizens throughout the world currently find themselves in. From a fiscal policy point of view, all is great as the green line of nominal values keeps growing, allowing governments to charge capital gains tax on top of the real world losses in purchasing power indicated by the red line. But time value of money is indifferent to the implications of inflation and merely ensures the black line of consistent valuations through time is flat-lining.

Summing up, the financial view of time value neglects inflation and is disconnected from the real economy. Arbitrage free pricing rules enforce a depreciation of future money balances at times of rising interest rates. But rising interest rates limit the speed of money creation and thus counter inflation, giving future money balances a higher value.

References

[1] Present Value, Wikipedia.org

[2] The Price of Time: The Real Story of Interest, Edward Chancellor, 2022, Allen Lane