The asset valuation calculator determines fair asset prices based on the present value of generated income. Usage instructions and explanations of the underlying mathematical formulas follow after the calculation form.
Usage Instructions for the Asset Valuation Calculator
Please fill the calculator form with the height of income payments or cash flows that the asset currently generates, the number of such income payments per year, your required return on investment, and the growth rate of income payments. All fields above the calculate button refer to input values, that you can change as needed. From these inputs the form calculates a fair asset value.
Depending on the type of asset, the income could be dividends, retained earnings or rent. In the case of rental income, the rate of inflation could be an appropriate estimate for growth. For stocks, on the other hand, a business analysis is preferable. Finally, we need to find our required rate of return.
The required rate of return is what makes an investment in an asset profitable. It usually follows from bond rates with an added risk premium. For instance, you could use 10 year treasury rates as a lower limit for the return. Next, you need to select an asset class for the risk premium. Growth stocks should be riskier than value stocks, which, in turn, are riskier than real property.
The valuation only works with required returns above growth rates. Otherwise, asset values grow to infinity and become purely speculative. This next section explains this economic problem in detail.
Fair Value of Speculative Assets
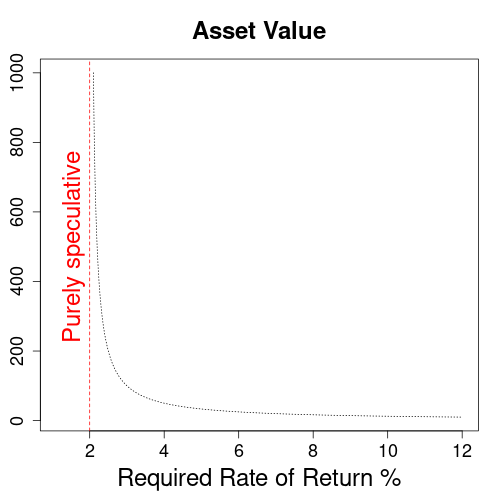
Estimating a reasonable asset value from expected income is not always feasible. Specifically, asset values grow to infinity when the required rate of return approaches the growth rate for income. In the above graph you see this behavior for a sample stock with dividends growing at a rate of 2%. Note that the asset value on the vertical axis is same as the price/earnings ratio (PE), since the stock pays a first dividend of $1. So as the required return closes in on 2%, the stock rapidly enters bubble territory with PE rations of over 500.
Of course, because of inherent risks a required return of just 2% is an input error for stocks. However, for growth stocks the purely speculative range starts at higher rates of return. Furthermore, whenever the FED decides on another round of QE, required returns drop. This might be a good explanation why certain tech stocks went ballistic in 2021.
How the Valuation Works
Investors buy assets because they want to make money. That is, they seek to find good investments where the compensation is higher than the purchase price. Therefore, it makes sense for investors to evaluate a fair market price for the income that assets produce. Afterwards, they can select buying opportunities by comparing asset prices to the fair value of income.
In order to estimate a fair price, the asset valuation calculator assumes that assets generate income in eternity. Even though nothing lasts forever, this method produces useful results. In fact, it turns out that income from a far future has negligible impact on the price assessment.
Mathematically it can be shown that under the assumption of a required return r an income C0 growing at an annual rate of g has the following fair value P:
P = C0 / (r - g)
Now, if we haven an idea of the regular income from an asset, such as dividends or rents, we can estimate its fair price. In addition, all we need are further estimates of an applicable rate of return and the expected growth.
Valuation of a Perpetuity
Let’s get some quick intuition on the valuation of income earned in eternity. Assume we deposit an amount X into an account paying out annual interest at rate r. If we never withdraw the amount X, then the account pays a constant annual income C in eternity:
C = X * r
Obviously, the constant earnings C are just the deposited amount X times interest r. Now, what would be a fair value for the annual earnings of C in eternity? For that, we rearrange the formula:
X = C / r
Clearly, given an interest rate of r, the fair price for eternal income C must be X. In finance, X is the value of a so-called perpetuity.
With a simple extension, we arrive at the formula that the asset valuation calculator uses:
P = m * C0 / (r - g)
P: asset price
C0: income at present time
m: number of income payments C0 per year
r: applicable rate of return
g: annual growth rate of income C0References
Rate of Return Pricing: Wikipedia.org
Similar Computations
Property Valuation in German: Zinseszins.de