The pension present value calculator determines the current value of long-term pension entitlements. It converts constant, regularly drawn payments into a one-time payment that is drawn immediately. An example application would be an option to have a pension insurance paid out as an immediately due severance payment. Usage instructions and explanations on the present value of annuities follow after the calculation form.
Usage Instructions for the Pension Present Value Calculator
Please fill the form with the pension payment that you regularly receive, an applicable nominal interest rate, and the number of years the pension is drawn. All fields above the calculate button refer to input values, which you can change as needed. From these inputs the calculator computes the present value of the pension.
Furthermore, you can choose to override the number of pension payments per year. The form sets a default of twelve, which will be appropriate for most users.
As an applicable nominal interest rate you could either pick a long term expectation of the inflation rate, or an interest rate that financial markets currently pay for investments.
Time Value of Money
The present value conversion of pension payments is based on the financial concept of time value of money. Time value of money considers how time affects the real value of nominal amounts of money. Take for instance a current amount X growing with compound interest to a higher value X+. So X is what you pay today in order to get X+ in the future. Therefore, the current price of the future amount X+ must just be X. In an analogous manner, you should pay a lesser amount X- in order to get a future amount of X.
The longer we invest a current amount X with compound interest, the higher its future value X+. Conversely, the further into the future we receive an amount X, the lower its discounted current value X-. This applies to each and every payout from the pension. As a consequence, current valuations of pension payouts are decreasing with time.
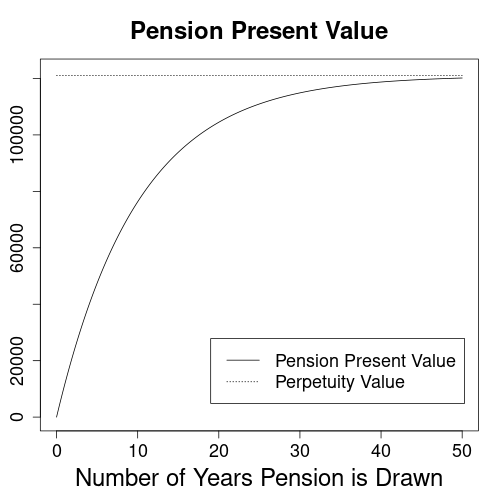
The effects of payout values decreasing with time can be seen in the above graph. At an interest rate of 10%, a monthly rent of $1000 received in perpetuity would have a present value of $121,000. As the benefit period keeps growing, the pension value approaches this theoretical maximum.
With 10% interest it’s of surprisingly little importance whether you live to enjoy your pension for 30 or 50 years. Of course only from a financial point of view! Note, however, that an interest rate of 10% is not unrealistic if the pension is valued based on the rate of inflation. After all, we are living in times of loose monetary policy.
How Inflation Eats up Pension Values
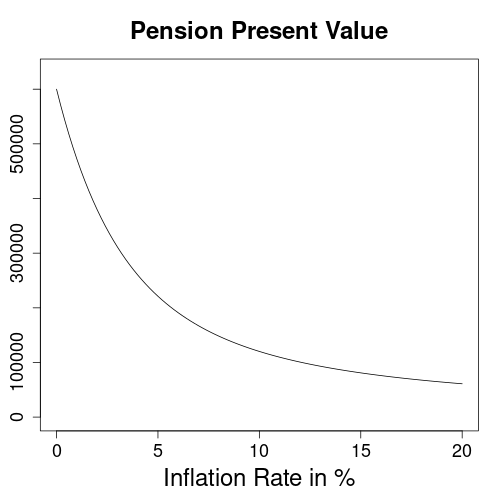
Finally, consider the impact of inflation on a pension drawn for 50 years. Monthly payments of $1000 would add up to $600,000 for a stable currency. However, with 20% inflation, this reduces to just $60,997. Therefore, pensions with constant payments do not protect well from poverty at old age. It’s much preferable to acquire inflation indexed claims.
Mathematical Formula for Pension Present Value
Mathematically, the problem of discounting every single pension payment with a different factor reduces to a simple formula for the overall value:
PV = (1 + r/m) * C0 * m/r * (1 - (1 + r/m)-m*t)
PV: Pension present value
C0: Constant pension payoff
r: applicable interest rate
m: number of payouts per year
t: number of years pension is drawnReferences
Time value of money: Wikipedia.org
Similar Computations
Present value: finalgebra.com
Pension present value in German: zinseszins.de