This interest calculator determines the present value of future income. In other words, this calculator tells you what money coming available in the future is worth at present time. Usage instructions and explanations of the underlying mathematical formulas follow after the calculation form.
Usage Instructions for the Present Value Calculator
Please fill the calculator form with an amount of future income, a nominal interest rate, and the number of years until receipt of payment. All fields above the calculate button refer to input values, which you can change as needed. From these inputs the calculator determines the present value of the future income. The discount factor is shown as a second result.
The compounding frequency setting adjusts the number of times per year of reinvesting interest income. It has a minor impact on results and most users will be fine with the standard value of once per year. However, you can overwrite this to twice (every six months), four times (quarterly) or twelve times (monthly).
Time Value of Money
The present value conversion of future income is based on the financial concept of time value of money. Time value of money considers how time affects the real value of nominal amounts of money. Take for instance a current amount X growing with compound interest to a higher value X+. So X is what you pay today in order to get X+ in the future. Therefore, the current price of the future amount X+ must just be X. In an analogous manner, you should pay a lesser amount X- in order to get a future amount of X.
The financial expression for the conversion of future income to a lesser present amount is discounting. Here, we multiply future income with a discount factor in order to compute its present value. Since this method works with any future amount, the discount factor is a more general result than the present value of a particular amount of future income.
We can fit discount curves to discount factors. Since the resulting curves are continuous, they will have discount factors for any point in time within the fitted interval. Therefore, discount curves are very useful in finance for the pricing of complex financial instruments. They are moreover independent from day counting or compounding conventions and thus a popular data format for the storage of yield curves.
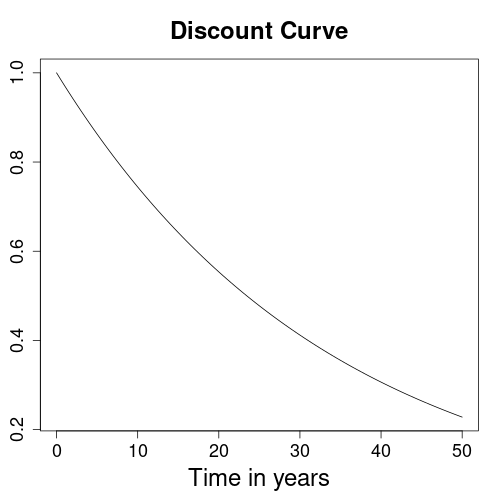
Due to its derivation from a constant interest rate, the above discount curve is an exponential decline. The discounting formula of the present value calculator produces the same type of curve.
Mathematical Formula for Present Value
The present value calculator form uses the following formula:
PV = FV * (1 + r/m)-m*t
PV: present value
FV: future value
r: interest rate
m: compounding frequency
t: time in yearsReferences
Discounting: Wikipedia.org
Similar Computations
Inflation calculator: finalgebra.com
Present value calculator in German: zinseszins.de