This financial calculator determines the height of installment payments for an installment loan. It is applicable to loan types with fixed interest and constant installments, such as mortgages, car loans and consumer credits. Usage instructions and explanations on the economics of installment loans follow after the calculation form.
Usage Instructions for Height of Installment Calculator
Please fill the Height of Installment Calculator form with the amount of the loan paid out to you, the outstanding loan amount at end of term, the loan interest rate, and the term of the loan in years. All fields above the calculate button are input values, which you can change as needed. From these inputs the form will calculate the required height of installments.
The term of the loan is same as the contract duration, or the number of years you will have to pay off the loan.
Per default, the form sets twelve annual installments equivalent to monthly payments in its number of installments input field. Since mortgages or car loans usually require monthly payback, most users will be fine with this setting. However, you may override this to four (quarterly payments), two (semi-annual payments) or one (annual payments).
In addition to the height of installments, the calculator outputs intermediate loan balances in the details section. Since this list can grow quite long, you may choose to hide it clicking the “hide -” label in its upper right corner.
Amortization Dynamics of Installment Loans
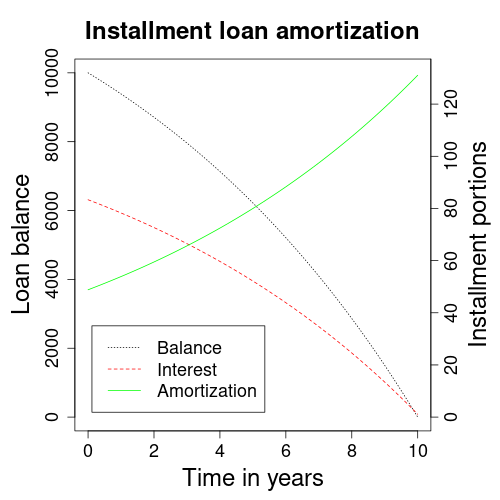
The above graph shows the amortization dynamics of a sample loan contract. Since the installments are much smaller than the initial loan balance, left an right hand axes have different scales. Measured by the right axis, interest payments are dashed red and amortization is solid green. The dotted black line in scale of the left axis is the outstanding loan balance.
Because installments are constant, their interest and amortization portions add up to the same amount at all times. In contrast, the amortization speed keeps increasing with time. Both the downward curved loan balance and upward sloping amortization lines confirm this behavior in the plot.
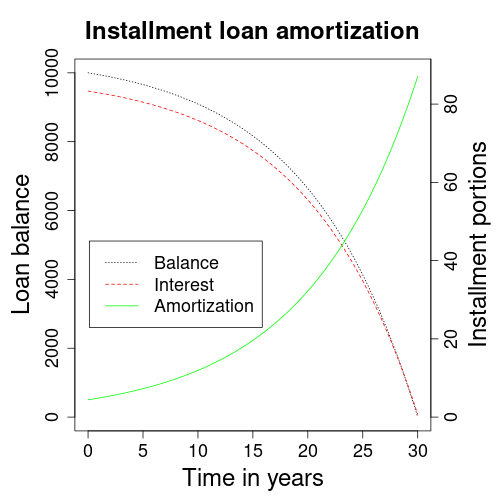
The second plot shows an installment loan as before, but with 30 years amortization. The longer contract duration reduces installments to $87.76, down from the $132.15 we had with 10 years amortization. However, the first installment pays off only $4.42 after the first month, down from $48.82 with 10 years amortization. Therefore, despite the lower installments, the total of interest payments is way higher with 30 years amortization. They climb from $5,858.00 with 10 years to $21,593.60 with 30 years amortization.
In short, the more time you have to pay back the loan, the more expensive it gets.
Mathematical Formula for the Height of Installments
The height of installment calculator uses the following formula to calculate installments:
Inst = r / m / ((1 + r/m)(m*t) - 1)
* (L0 * (1 + r/m)(m*t) - L1)
Inst: installment amount
r: interest rate
m: number of installments per year
t: duration of loan contract in years
L0: loan amount paid out at start
L1: remaining loan balance at end of contractReferences
Mortgage Loans: Wikipedia.org
Similar Computations
Heigt of Installment Calculator for Installment Loans in German: zinseszins.de